���ی���Ñ�w�@���v�w�Q�O�P�U
�i�ی���Êw�����n�r���e�[�V�����w�ȁ@���w�Ö@�w��U�E��ƗÖ@�w��U�j
�V���o�X
�J�u�ɂ�����܂��ĂQ�O�P�U
��1��@�덷�ƌ�
���B�ڕW�P�|�P�^�x�������������l���邱�Ƃ��ł���
�P�|�Q�^�x�������������l���邱�Ƃ��ł���
�P�|�R�𗍂ɂ��ė�������������邱�Ƃ��ł���
�덷
���R�덷�ƌn���덷�ɕ���������R�덷�E�E�E���x�̘b
�n���덷�E�E�E�^�x�̘b

���x�̌���
���R�덷�̔r���@�@ ���R��������덷�E�E�E�m���_
�̉��v�E�E�E����ꏊ���ɂ��Ă������ł��Ӑ}�����ɔ����ɂ����
���S�Ɍ��藝
�W�{�̑傫�����\���ł���ΕW�{���ς̕��z�͐��K���z
�����������肳��Ă���̂ł�����R�덷�̔����͐��K���z�ɏ]��
������𑝂₹�Α��₷�ق�
���Q�l��
http://aoki2.si.gunma-u.ac.jp/lecture/SampleSurvey/samplesize.html
�^�x�̌���
�n���덷�̔r�����R�ł͂Ȃ��i�K�R�́j�덷�ւ̑Ή��E�E�E��i�o�C�A�X�j�̏���
�I���̕�
�����������Â��Ă���A�f�f�����₷�������B
���̕� ���U�̕Ƃ�
�𗍈��q
�u�w�ł��ڂɂ����錾�t���C�^�[�����Ɣx����ɂȂ�H�H�H�i�댯���q�j
���̏ꍇ�A�i�����𗍈��q
�𗍈��q�Ƃ�
�E���a�����̊댯�v���E���I�i���C�^�[�j�Ɗ֘A������
�E���I�i���C�^�[�j�Ǝ��a�̒��ԉߒ��ł͂Ȃ�
��2�`5��@�m���I���_
���B�ڕW�Q�|�P���x�Ɠ��ٓx�̎Z�o���o����
�Q�|�QROC�Ȑ���������
�Q�|�R�x�C�Y�̒藝��p�����v�Z���s����
�m��
P(A)�E�E�E����A���N����m��P(A|B)�E�E�E����B���N���������Ŏ���A���N����m��
���x�Ɠ��ٓx
���x��P(�z��|�c)�U�z������P(�z��|�cc)
���ٓx���P�|�U�z����
���ł��z���Ɣ��f���錟���͊��x���U�z�������P�ɂȂ�
�i�Ȃ�ł�����ł��A����܂�!�I�@�̃m���j
ROC�Ȑ�
���o�\�̕]�� ���x�Ɠ��ٓx�i�P�|�U�z�����j��p���ċȐ���`���x�C�Y�̒藝
P(A|B)�̐��E�̎��Ԃ̌����ɂ���P(B|A)�̐��E�����O�m���i��F��ʂɜ늳����m���j���f�[�^�i��F�������ʁj������m���̎Z�o
���B�x�m�F
�P�jA����͐��уW���[���ɏ��X�X�ɍs�����Ƃ��Ă��܂��BA���X�X�ł͐��уW���[����20%�̊m���Ōi�i�i��5kg�j�̂����钊�I��ł��������������Ƃ��ł��܂��B
���B���X�X�Ŕ�����10%�̊m���Ōi�i�i��10kg�j�̂����钊�I��ɎQ���ł��܂��B
A���X�X�̕����i�����������邽��60%�̊m���ōw���A
B���X�X�̕��͎���i�������̂ł����i���L�x��40%�̊m���ōw������Ƃ����ꍇ�A
A���i�i�i�āj����ɂ���m���͉����ł��傤���B
�Q�j�ȉ��̃}�����O���t�B�Ɋւ��錟�����ʌ��ʂ���ROC�Ȑ���`���A���ȏ�P13�̌��ʂƔ�r���Ăǂ���̐��\��������Ă��邩�q�ׂ�
�E�N���b�N�Ń_�E�����[�h
��͈ȉ��i�����͎��Ƃɂĉ���j
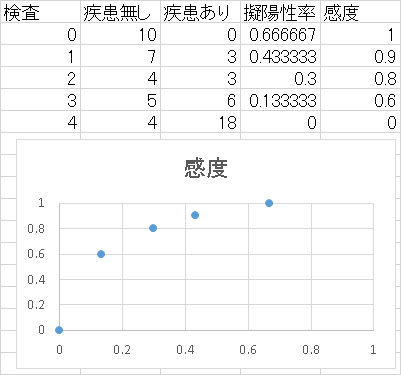
�R�j���ȏ�P9�\1.1�̃f�[�^��p���ăx�C�Y�̒藝��p���ėz���I���������߂�
�⑫
|
���ȏ��Y���y�[�W 1��P2-P22 ROC�Ȑ��̕]���͖ʐς̘b�ƍ���ɋ߂��Ȑ��̕���������Ă���Ƃ����b �J�b�g�I�t�|�C���g�̘b�����܂��� ��ʓI�i���ȏ��I�j�ȗ����͂���ŗǂ����Ǝv���܂� �������A�ړI�ɂ���Ęb���x�����߂ɂ��邱�Ƃ��U�z���̔��������D�悷��ꍇ������܂����A���̌����Ƃ̑g�ݍ��킹������̂ŗǂ��l����K�v�͂��� �Q�l�L���F ����̌����Łu�z���v�ƌ���ꂽ��A������̂��H�iMEDLEY�j https://medley.life/news/item/56a097e14f22981e008b4572 ���f�u�z���v�ł��X�X���͖��Ȃ��H�ӊO�ƒm��Ȃ��f�[�^�̐^�� http://bylines.news.yahoo.co.jp/mamoruichikawa/20160503-00057271/ ���x�E���ٓx�͎����̊m���Ɉˑ����Ȃ����A�\���l�͈ˑ�����Ƃ����b ������̓��� ��Q��F�m���̌v�Z�C���x���ٓx�̌v�Z�C�q�n�b�Ȑ��̍쐬 ��R��F�G�N�Z����p���đ�2��̕��K ��S��F�G�N�Z����p���Č[�f�[�^����ROC�Ȑ��̍쐬�i������p�����\�쐬�j ��T��F�G�N�Z����p���Č[�f�[�^����ROC�Ȑ��̍쐬�C�]�� ���K�ɂǂ��� �y���v�w�zROC�Ȑ��Ƃ͉����A�A�j���[�V�����ŗ�������B ROC�Ɋւ���b�͂��Ƃ��Έȉ��̃T�C�g�i���vWEB�iSSRI�j�j��������܂��B�G�N�Z���Ƀ\�t�g���A�h�C��������@������܂� https://software.ssri.co.jp/statweb2/sample/example_25.html |
��6�`7��@�L�q���v
���B�ڕW�U�|�P�[����x�����z�\���쐬�ł���
�U�|�Q��\�l���Z�o�ł���
�U�|�R�U�z�x���Z�o�ł���
�U�|�S�W���덷�A���S�Ɍ��藝�ɂ��Đ����ł���
�x�����z
�ȉ��̓x�����z�\�̃t�H�[�}�b�g�ɏ]�����ȏ�P23��PCB�̑���l�ɂ����P�D�x�����z�\�̍쐬
�@�@�[�f�[�^����J�E���g�����邱��
�Q�D�q�X�g�O�����̍쐬
| �K�� | �K���l | �x�� | ���Γx�� | �ݐϓx�� | �ݐϑ��Γx�� |
|---|---|---|---|---|---|
| 0-2.5 | |||||
| 2.5-5 | |||||
| 5-7.5 | |||||
| �v | ----- | ----- | ----- |
��\�l�̎Z�o
���ϒl�͌[�f�[�^�y�ѓx�����z�\���狁�߂邱���U�z�x�̎Z�o
�W�{���U�ƕs�Ε��U�ɒ���������p�����藝�̊m�F
�E���S�Ɍ��藝�E�W�{�덷�ƕW����
�⑫
|
���ȏ��Y���y�[�W 2��P23-P31 3��P70-71,P85-P97 ������̓��� ��U��F�x�����z�\�̍쐬�A��\�l�̎Z�o ��V��F�U�z�x�̎Z�o |
��W��@����i�T�j�@��A����
���B�ڕW�W�|�P��A�����̐ؕЃ�0�ƌX����1�����߂���
�W�|�Q�s�A�\���̑��W���ɂ��Đ����ł���
�W�|�R����W���i��^���j�����߂邱�Ƃ��o����
�f�[�^���疢�m�p�����[�^�̐���l�����߂�
�ŏ����@
�덷�̓��a���ŏ��ɂȂ�悤�ɐ��肵������P119�̗�5.2��藝5.3��p���ċ��߂�
�G�N�Z���ŎU�z�}��`���Ă݂ē��l�Ȍ��ʂɂȂ邱�Ƃ��m�F����
���W��
��1������ΐ��̑��ւ�����̂����̑��ւ�����̂���������̂�X��Y�̊֘A�̋����܂ł͕�����Ȃ����W��r��-1�`1���̒l�����Ƃ�Ȃ��B
�����g�킸��P119.��5.2����s�A�\���̑��W�������߂�
���Q�l������ ��ナ�n�r���e�[�V�������w�Z�@���v�w�Q�O�P�T�i���w�Ö@�w�ȁj���Ǝ������Q�l�ɂȂ镔��
http://www.medbb.net/education/ocrstat2015/index.html#4
��X��@����i�U�j�@��Ԑ���
���B�ڕW�X�|�P�ꕪ�U�����m�̏W�c�̕ꕽ�ς̋�Ԑ��肪�ł���
�X�|�Q�ꕪ�U�����m�̏W�c�̕ꕽ�ς̋�Ԑ��肪�ł���
���ȏ�P126�`
�ꐔ������m���œ��镝������������l
�ꕽ�ς͈�肾���W�{���ς͕W�{���ɈقȂ�
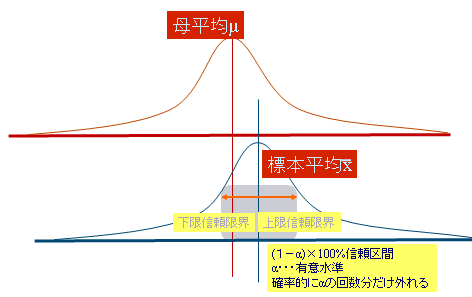
�W�{���ςɕ����������邱�ƂŁA���̘g���ɕꕽ�ς�����
���K���z
���E�Ώ̂̒ޏ��z�i���ȏ�P34�j���ϒl�ɋ߂��قǏo������������������ɏ]���ĒႭ�Ȃ�i���Ƃ������j
�������m�������ŌJ��Ԃ��Ɛ��K���z�Ƃ����b
�W�����K���z
���ϒl���O�W�������P�i���U���P�j�ɂȂ�悤�ɒl��ϊ���������
���l�͕��ϒl��50�A�W�������P�O�ɂȂ�悤�ɒl��ϊ���������
�W�����ƕW���덷
�E�W�����͕W�{�̕��z�̃o���c�L��������������E�W���덷�͕�W�c���璊�o�����W�{�̕��ϒl�̃o���c�L�
SE=�Ё^��n
�����ߋ��ɗ��R����������Ƃ��̎��� http://www.medbb.net/education/ocrstat2015/index.html
��W���������m�̏ꍇ�̋�Ԑ���
���K���z�͕ꕽ�ϒl�ƕ�W������������Ȃ��Ǝg���Ȃ���n�������ꍇ�W�{���ςƕW�{�W�����ŋߎ��ł��邪n�����Ȃ��ꍇ�͋ߎ��ł��Ȃ���t���z(�W�{�̎��R�x�˂����킩���Ă���A��͌��蓝�v�ʂ����߂�Ίm�����킩��)
�����z
���R�x�݂̂ł��܂�m�����z
���R�x�E�E�E�W�{�̒��Ŏ��R�ɐU�镑�����Ƃ�������Ă���̂̐�
�@�@�@�@�@�@���v�l���ꐔ�̐���ƂȂ�ƁA���R�ɐU�镑���Ȃ��̂��o�Ă���i���܍��킹�j
�W�{���U�͕����a���̂̐��ŏ����邱�Ƃŋ��߂邪�ꕪ�U�̂قǂ悢����ł���s�Ε��U��n-1�i���R�x�j�ŏ�����
��
�ꕪ�U���m�@NORM.S.INV�ꕪ�U���m�@T.INV.2T
P135�\5.7
�@
��P�O�`�P�P��@t����
���B�ڕW�P�O�|�P��������̎菇�ɂ��Đ����ł���
�P�O�|�Qt������s�����Ƃ��o����
��������
����O��݂����Ɍ��肷��̂ł͂Ȃ��A���肷�闝�R�E�m�M�����邩��m���߂�@�Ƃ����������菇�P�F���������Ă�i�A������H0����ёΗ�����H1�j
�w���@�Ɋ�Â��ؖ������Ă���B
�i�����Ȃ��������ؖ��ł��Ȃ��̂ŁA���̑Η��ł��鍷�����鉼�����̑�����j
�菇�Q�F�L�Ӑ��������߂�
�m���I�ɕK�R�Ƌ��R��蕪���Ă���B��ʂɂT���ŕ����Ă��邪�P���̎�������
�菇�R�F���蓝�v�ʂ��v�Z����
���̎��ۂ̋N����m�����v�Z���Ă��邱�ƂɂȂ邪�A�p����m�����z�ɂ���Čv�Z�����قȂ�B
�菇�S�F�L�Ӑ����Ɣ�r���A���������p�̑�����
��j�A������H0�����p���Η�����H1�̑�
t���z
���K���z�Ɋ�Â��m�������߂�ɂ͕ꕽ�ςƕ�W�������K�v��n�������ꍇ�W�{���ςƕW�{�W�����ŋߎ��ł��邪n�����Ȃ��ꍇ�͋ߎ��ł��Ȃ���t���z(�W�{�̎��R�x�˂����킩���Ă���A��͌��蓝�v�ʂ����߂�Ίm�����킩��)
���R�x
�l�����E�E�E�W�{�̒��Ŏ��R�ɐU�镑�����Ƃ�������Ă���̂̐�
�@�@�@�@�@�@���v�l���ꐔ�̐���ƂȂ�ƁA���R�ɐU�镑���Ȃ��̂��o�Ă���i���܍��킹�j
�W�{���U�͕����a���̂̐��ŏ����邱�Ƃŋ��߂邪�ꕪ�U�̂قǂ悢����ł���s�Ε��U��n-1�i���R�x�j�ŏ�����
t����̎��
��W�{�i�r�t�H�[�A�t�^�[�j�@��̏W�c��ΏۂƂ��Ă���̂Ŋy
��W�{�i�s�B�̏W�c���r�j
�@���ꂼ��̏W�c���ꏏ�ƌ��Ȃ��ėǂ���
���Q�l���Ƃ肠�������������Ă݂��Ƃ������v�̘b�imedbb.net�j
http://www.medbb.net/education/ocrstat2015/img/01toriaezu.pdf
���B�x�m�F
�P�F18�l�̊��҂�A�܂�1�T�ԓ��^���O��̖��������v�������BA�܂Ɍ��ʂ����邩������s���B��������ŗL�Ӑ�������0.05,0.01�Ō��肹��B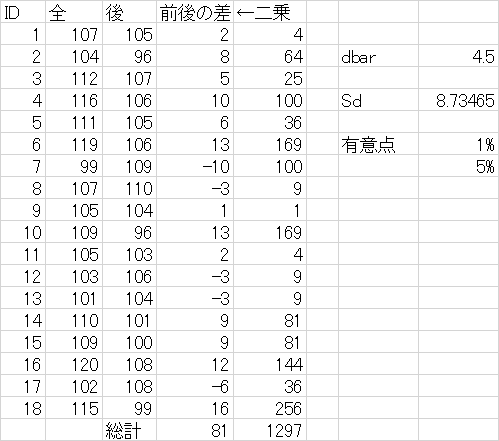
�Q�F����͂���a�@�i�]�ƎҐ�300�l�j�Ŏ��{�������N�f�f�ꕔ���i���ː����j�̐g���̋L�^�ł���
| ���� | �l�� | ���ϒl(cm) | �s�Ε��U |
|---|---|---|---|
| �� | 11 | 152.5 | 25 |
| �j | 13 | 160.3 | 9 |
�⑫
|
������̓��� ��P�O��F����̎菇�At���z ��P�P��Ft���� |
��P�Q�`�P�R��@�䗦�̌���
���B�ڕW�P�Q�|�P����
�P�Q�|�Q�J�C��挟����s�����Ƃ��o����
�P�Q�|�R���ڌ�����s�����Ƃ��o����
���z
���ȏ�P39���x���k�C���s���R�C���i�\������50%�j���g�X�����Ƃ��ɕ\���o��m�������߂�in=2,100,1000�j
P=nCi�~P^i�~�i�P�|p�j^(n-i)
nci��n!/(k!(n-i)!))
���၄
�R�C����2��g�X�����Ƃ��ɕ\��0��ɂȂ�m��
nci��2*1/(1*2*1)=1
P(i=0)=1*0.5^0*(1-0.5)^2=0.25
�R�C����2��g�X�����Ƃ��ɕ\��1��ɂȂ�m��
nci��2*1/(1*1)=2
P(i=1)=2*0.5^1*(1-0.5)^1=2*0.5*0.5=0.5
�R�C����2��g�X�����Ƃ��ɕ\��2��ɂȂ�m��
nci��2*1/(2*1*1)=1
P(i=2)=1*0.5^2*(1-0.5)^0=0.25
���ƂŃG�N�Z����BINOM.DIST�ł��m�F
P62�@���z�Ɛ��K���z
P176
=NORM.S.DIST(-2.58,TRUE)�@�Ƃ���������
�J�C��挟��
P180�o���x��Oi�Ɗ��ғx��Ei�̃Y��������
�J�C��敪�z�Ɛ��K���z�̊W���m�F
CHISQ.INV.RT
=NORM.S.INV
�o���x���Ɗ��ғx���̃Y���̘b
=CHISQ.TEST
���ڌ���
���̏��N����m���ڑg�ݍ��킹����v�Z���Әa���Œ肵H1�̕����i���ғx�����痣�������j�ɕς��Ȃ���v�Z���J��Ԃ�
���߂�ꂽ�m����S�Ă���
�����Η������̏ꍇ�A�Б��͂��̔���
| �L�� | ���� | �v | |
|---|---|---|---|
| A�Q | O1 | O2 | m |
| B�Q | O3 | O4 | n |
| j | k | t |
�⑫
|
������̓��� ��P�Q��F���z�C�J�C��敪�z ��P�R��F�J�C��挟��C���ڌ��� |
��P�S�`�P�T��@���܂Ƃ�
P102�\�S�D�Q���G�߂ɂ�蕽�Ϗo�Y���Ԃɍ������邩���肹��P102�\�S�D�Q���G�߂ɂ��ُ�o�Y�̏o���䗦�ɈႢ�����邩���肹��
P102�\�S�D�Q�y�ѕ\�S�D�R���G�߂ɂ�蕽�Ϗo�Y���Ԃɍ������邩���肹��
P102�\�S�D�Q�y�ѕ\�S�D�R���~���ɂ����ďo�Y�ꏊ�ɂ�蕽�Ϗo�Y���Ԃɍ������邩���肹��